![[딥러닝] #5 퍼셉트론(Perceptron)에 대해서 알아보자 / 인공신경망(ANN) 퍼셉트론과 뉴런의 차이점 / 편향 b(bias)의 의미](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbBTbka%2FbtqHvLAb06h%2FvzIYAGWyz7SPnoHnpNXbeK%2Fimg.png)
오늘은 신경망 알고리즘에서 가장 많이 등장하고 기초적인 개념이 되는 퍼셉트론(Perceptron)에 대해서 알아보자. 일단 퍼셉트론이 뭔지 자세히 알아보기 전에 어떤 부분에서 퍼셉트론이라는 개념이 쓰이는지 간단하게 보고 넘어가자.
퍼셉트론(Perceptron)은 인공신경망(ANN)을 구성한다.
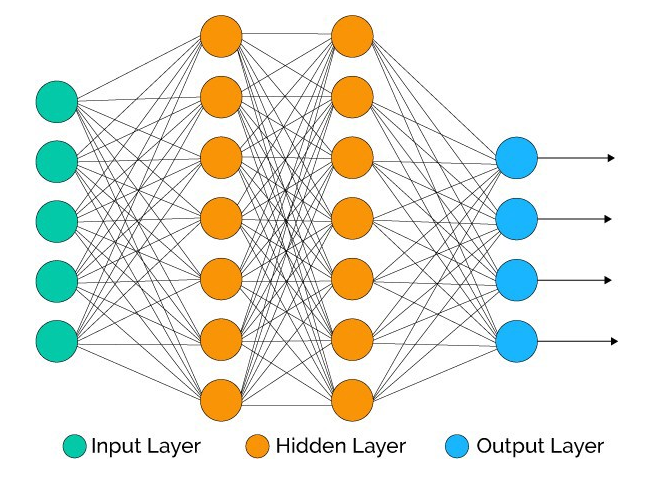
저번에 우리가 인공신경망이 무엇인지 알아보았다. 간단하게 요약하자면 인공신경망은, 인간의 신경세포 뉴런이 자극을 전달하는 일련의 과정들을 모방해 만든 인공적인 모델이라고 했다. 신경자극 전달을 몸에서는 뉴런(Neuron)이라는 신경세포가 했듯이, 인공신경망에서도 인공뉴런이 있다고 했다. 그 인공 뉴런이 바로 퍼셉트론이다.
위에 인공신경망 예시사진을 첨부했는데, 저기서 구성하는 원들이 퍼셉트론이라고 생각하면 된다.
뉴런(Neuron)과 퍼셉트론(Perceptron)의 차이점
퍼센트론 = 뉴런
그럼 인간 몸의 신경망을 구성하는 뉴런과, 인공신경망을 구성하는 인공뉴런의 차이가 뭘까? 일단 헷갈리지 않기 위해 공통점을 집고 넘어가자. 둘 모두, 여러 자극(Input)을 받아들이고 다음 뉴런으로 자극을 전달한다. 사실 역할이나 구조가 동일하다. 따라서 뉴런 = 퍼셉트론으로 이해해도 괜찮다.
하지만 인공 뉴런이아닌 퍼셉트론으로 이름을 붙인 이유가 있을것이다. 뉴런은 인간 몸에서 자극을 전달하는 생물학적, 화학적인 개념이고, 퍼셉트론은 이 과정을 수학적으로 모델링한 개념이다. 음.. 이해가 좀 안가려나..? 그러니까 뉴런은 실제 우리 몸에있는 말랑말랑하고, 사람이 인공적으로 만들 수 없는 그 생물학적 뉴런 그 자체고, 이걸 인공적으로 만들기위해 수학적인 개념을 동원하여 뉴런처럼 동작할 수 있게 구현해 놓은 '수학적인 모델'이 바로 퍼셉트론이다!!
퍼셉트론(Perceptron)의 기본 동작 원리
위에서 말했듯기 생물학적인 뉴런의 작동방식을 인공적으로 만들어낸게 바로 퍼셉트론이라고 했다. 인공 뉴런이라고 부르지않고 수학적인 개념이기 때문에 퍼셉트론이라는 다른 이름으로 불린다고도 했다.
저번 포스팅을 보면 뉴런이 어떻게 동작하는지 알아봤다. 기억이 안난다면 이전 포스팅을 참조하기 바란다. 생물학적인 뉴런의 동작방식을 간단하게 살펴보자면, 여러개의 가지돌기들에서 자극(Input)을 받아들이고 그 가지돌기들 중 중요한 신호를 받아들이는 가지돌기들은 가중치가 높은 가지돌기들이라고 했다. 그리고 그 자극들의 총합이 해당 뉴런의 활성화 함수 임계치를 넘게되면 뉴런이 활성화되어 촉색돌기로 신호를 뱉어 다음 뉴런으로 자극을 전달한다고 했다.
그럼 퍼셉트론도 이런 구조로 되어있는지 위 사진을 보며 비교해보자. 자극이 들어오면 퍼셉트론의 앞단에서 각 가중치에 맞게 입력을 받아들인다. 받아들여진 가중치가 곱해진 입력들의 합은 활성화함수(임계함수)를 통과해 해당 퍼셉트론을 활성화할지 말지 정해준다. 만약 입력의 총합이 해당 퍼셉트론의 활성화함수 임계치를 넘으면 출력을 1로 뱉어 다음 퍼셉트론으로 자극을 전달한다. 반대로 임계치를 넘지 못하면 출력은 활성화되지 않는다.
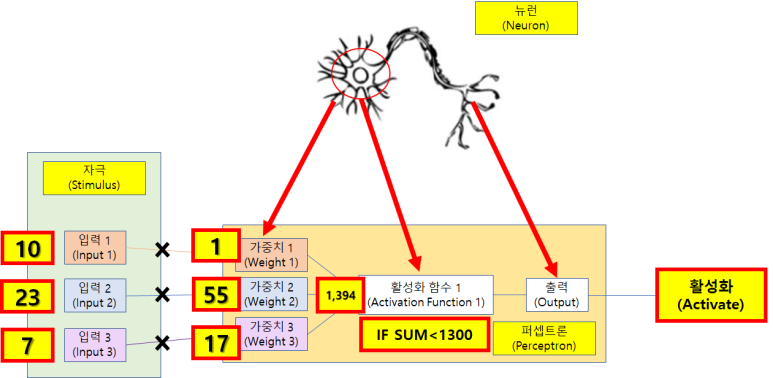
예시를 들어보자. 자 입력에 10, 23, 7의 자극이 들어왔다. 각 가지돌기의 중요도에따라서 1번 가지돌기는 가중치가 1로써 그렇게 중요하지않은 가지돌기 같다. 두번째 가지돌기는 가중치가 55로써 세 가지돌기들 중 가장 높은 가중치를 가지고 있는것으로보아 가장 중요한 신호를 받아들이는 가지돌기로 판단된다. 마지막 세 번째 가지돌기는 가중치가 17이다.
자. 첫번째 가지돌기에 10이란 입력신호가 들어왔고 가중치가 1이니 총합이 10이다, 두 번째 가지돌기도 같은방식으로 23x55를 하면 1265라는 수치가 나온다. 세번째 가지돌기도 같은방식으로 7x17을 하면 119라는 값이 나온다. 그럼 이 세 가지돌기에서 가중치를 고려해 모든 자극의 합을 보면 10+1265+119 = 1394라는 값이 나온다. 해당 퍼셉트론이 입력을 통해 받아들인 가중치를 고려한 입력들의 합은 총 1394라는 것이다. 저기서 활성화 함수를 보면 조건이 IF = 만일 / SUM<1300 = 총합이 1300보다 크면이라는 조건이 있다. 현재 총합이 1394이기 때문에 해당 조건을 만족하니 출력이 Activate 되는 것이다.
엥? 엄청 간단하잖아? ..!!? 맞다. 왜 수학적으로 모델링 가능한지 감이 왔을것이다. 단순히 입력값들에 가중치를 곱해주고, 그걸 다합쳐서 활성화 함수를 만족하면 활성화시키고 아니면 활성화시키지 않고, 단순하다. 나중에 배우겠지만 어려운건, 이걸 어떻게 학습하는 퍼셉트론으로 만들꺼냐인데 이건 나중에 아주 천천히~ 배워보자.
더 구체적인 퍼셉트론(Perceptron)
위 퍼셉트론 구조에서 새로운 개념이 추가됐다. 가운데 보면 편향(bias)라는 개념이 추가됐다. 편향은 뭘까? 해석하자면 해당 퍼셉트론(뉴런)이 얼마나 쉽게 활성화 되는지를 조절하는 조절하는 매개변수정도로 생각하면 된다.
엥?? '얼마나 쉽게 활성화 되는지?' 이게 뭔말이야! 라고 생각하는 사람을 위해서 간단한 설명을 더 해보겠다. 일단 활성화 함수의 임계치가 1300이니, 자극의 총합이 1300이 넘어야 뉴런이 활성화 된다. 여기서 편향이 1이라고 하면 이 뉴런이 받아들인 자극들은 입력 1~3에서 들어온 값에 가중치가 곱해진 합이니, 즉 입력에 의존하게 된다. 쉽게말하면 입력의 강도들이 적으면 당연히 총합도 줄어드니 1300에 도달하기 힘들것이다.
하지만 편향이 500이라고 가정해보자. 그럼 입력 1,2,3이 모두 0이 들어와도 편향이 500이니 입력값 총합 0 + 500 해서 아무것도 안했는데 입력의 총합이 500이 되버리는 것이다. 뭐 극단적인 예시긴 한데ㅋㅋㅋㅋ 일단 공짜로 500먹고 시작하니 입력값에 의한 의존도가 상대적으로 줄어드는 것이다.
더 강한 예시를 들자면 편향이 1200이라고하자, 그럼 입력1~3이 각 가중치가 곱해진 총합이 100만 넘으면 뉴런이 활성화 되는 것이다. 그럼 처음에 말했듯이 아주쉽게 뉴런이 활성화 되는것으로 해석할 수 있다. 편향이 1일때는 입력값과 가중치 이것저것 다 곱해서 또 다더한후 1300이란 값을 만들어야 활성화 됐는데 편향이 높으면 대충 해서 입력들x각 가중치 해서 100만 만들면 편향이 1200이니 쉽게 활성화 되는것이다. 이제 좀 이해가 됐을 것이다.
편향 b(bias)의 의미
= 퍼셉트론이 얼마나 쉽게 활성화 되는지의 정도
편향이 있는 이유는 해석하자면 얼마자 쉽게 활성화 되는지를 조절한다고 하지만, 이것은 오차를 고려한 것이다. 입력 강도를 매개변수(입력들)들과 가중치를 합한것으로만 다루면 좋지만, 매개변수에서 예상하지 못한 잡음(노이즈)을 제거하기 위한 이유도 있다. 예를들어 입력을 받아들이는데 노이즈가 생겨 30정도의 값들은 아무것도 안했는데도 들어온다면 편향에 30을 주어 그 노이즈로 들어온 30을 무시해주면 되는것이다.
이것을 수학적으로 표현하자면 저 편향은 선형그래프에서 y절편이 된다.
활성화 함수(Activation Function)은 무엇일까?
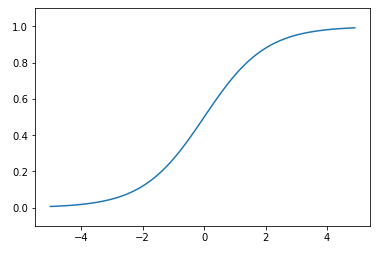
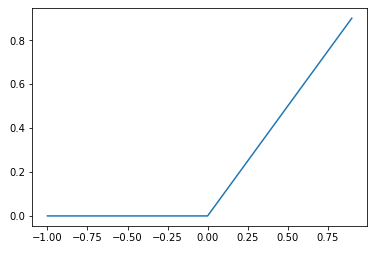
자 퍼셉트론이 여러가지 입력을 받아들인뒤 가중치를 곱해 합쳐진 값이 활성화함수(Activation Function)을 지나 출력을 줄지 말지 정한다고 했다. 풀어서 이야기하자면, 활성화 할지는 1이고 말지는 0이다. 그렇다 어떤 값이 들어오던 결과로 1(활성화) or 0(비활성화) 이렇게 두가지로만 나오면 된다. 그 역할을 해주는게 바로 활성화 함수다.
그래프들을 보면 모두 y축 출력값이 0~1인 것을 알 수 있다. 그래프가 여러가지가 있는데 첫 번째 스탭 함수를 보면 출력이 0과 1밖에 없다. 이게 방금말한 활성화 할지, 말지 딱 두 종류만 반환해주는 함수다.
다음 시그모이드 함수를 보면 0~1사이에 실수의 값들이 채워져있다. 예를들면 0.45 , 0.77 등, 이경우는 활성화 됐다, 안됐다가 아닌, 활성화 정도를 반환해주낟. 1에 가까우면 많이 활성화 됐다는 것이고 0.2 이렇게 반환되면 적게 활성화 된거고, 연속적인 성격을 뛴다.
마지막 렐루함수는 0이하일때는 0 그 이상일때는 입력그대로가 나온다. 요즘에는 이 함수를 활성화 함수로 많이 쓴다고 한다. 0 밑으로는 무조건 다 비활성화를 시키고, 0 이상은 입력 그대로가 출력으로 작동해 값이 크면 클수록 활성화가 강력히 되는 친구다.
뭐, 복잡해보이지만 활성화 함수는 입력으로 어떤 숫자가 오던 출력으로는 0과 1사이의 값만 반환하는 것이다. 이 활성화 함수가 있기떄문에 인간의 뉴런이 활성화 될 때를 구현할 수 있는 것이다. 여기서 알아야할 것은, 이 활성화 함수를 통해서 복잡한 입력값들의 합이 간단하게 0~1사이로 아주 간단하게 바꿔준다는 것. 이것만 알고가자.
퍼셉트론(Perceptron)을 수식으로 표현해보자!
자 우리가 지금까지 봤던 저 퍼셉트론을 수학적으로 표현해보자. 복잡해보이지만 우린 충분한 설명을 거쳤기 때문에 식을보면 이해가 갈 것이다.
후... 수식 입력하는 사이트에서 손수 입력해서 왔다. 여기서 딱보고 앗.. 시그마는 그래도 고딩떄 본거 같은데 그래도 익숙하지가 않네..? 하시는분들 계실꺼다. 나도 너무 오랫만에 수식을봐서 적응이 안됐었다. 먼저 좌변부터 보면 y가 아닌 y위에 ^ 표시가 있는 y-hat으로 표현해놨다. 딥러닝 분야에서는 예측값이라는 의미로 y와는 구분된 y-hat으로 표기한다고 한다. 앞으로 y-hat이 나오면 예측값 정도로 해석하면 된다.
이제 가장 중요한 우변을 보자 일단 바로 b가 보인다. b는 편향이라고 했다. 퍼셉트론이 활성화되는 정도를 의미한다고 했는데 가장 맨 앞에 씌인 이유는 간단하다. 만약.. 시그마식 뒤에 b가 왔으면 시그마 식에 포함되어 있다고 착각하시는 분들이 많아, 그런 오해를 없애기 위해 맨 앞에 뒀다. 자 여기까진 어렵지 않을 것이다.
뒤에 시그마 식을보자. 자 n이 입력의 갯수고 입력이 1부터 n까지 들어왔다. 들어온 입력이 x1부터 xn까지다. 위에 사진을 보듯이 가지돌기 부분에 중요한 순서대로 가중치 W가 있다고 했다. 그 가중치들이 바로 Wn인거다. 보면 1번 입력 x1은 해당 가중치인 W1과 곱해질꺼고, x2는 W2와 곱해질꺼고 ...해서 xn은 Wn과 곱해질꺼다. 그리고 이 모든걸 합쳐준다. 이렇게 하면 우리가 위에서부터 계속 공부한 퍼셉트론 모델이 완성되는것이다.
이 시그마에서 합쳐진 자극신호들의 합과 편향까지 합치면 y-hat 즉 예측값이 나올꺼고 이걸 활성화 함수에 넣으면 출력이 0~1이 나오게 된다.
여기까지 퍼셉트론에 대해서 알아보았다. 후... 2일간 쓴 글이라 어꺠가 너무 아프다 ㅠㅠ
[딥러닝] #5 퍼셉트론(Perceptron)에 대해서 알아보자 / 인공신경망(ANN) 퍼셉트론과 뉴런의 차이점 / 편향 b(bias)의 의미
#딥러닝 #퍼셉트론 #인공신경망 #뉴런 #차이 #편향 #활성화함수 #기본 #기초 #원리