[딥러닝] #7 선형 회귀 (Linear Regression) 모델과 경사하강법 (Gradient Descent)의 의미

머신러닝을 포괄적으로 이해하자면 어떤 입력을 넣어 어떤 출력값이 나오는 모델을 만들껀데, 이 과정중 학습이라는 행위를 통해서 예측값을 더 정확하게 하는 과정이라고 보면 됐었다.

​

오늘 배울 것은 선형 회귀 모델로써 우리가 처음 배우기에는 가장 이해하기 쉬운 학습모델이다. 무작정 퍼셉트론을 이용해 인공신경망을 이해하려는것 보다. 가장 간단한 형태의 학습모델을 이해하고 차근차근 딥러닝 모델을 이해하도록 해보자.

선형 회귀 (Linear Regression)

선형함수의 기울기와 절편을 찾는 과정

선형 회귀. 딱 들었을때 아.. 수학이구나 하고 엄청 어렵겠다고 생각하는 사람이 꽤 있을것이다. 나도 어..머..딥러닝이 어려운거니까 분명 어렵겠지? 라는 선입견으로 한번 쭉~ 공부해봤는데 고등교육 수준선에서 충분히 이해할 수 있는 내용이다.

​

자 머..책이던 뭐 블로그던 선형회귀를 설명하면 보통은 선형회귀가 뭔지부터 설명한다. 그렇게 되면 처음 공부하는 사람으로써는 글로만보니 읽어도 감이 빠르게 오지 않는다. 그래서 감을 먼저 얻고 선형회귀를 이해하기 위해 아래 예시로든 사진을 살펴보자.

자 가로축은 입력 X다. 세로축은 입력 Y다. 와우 짱쉽다. 2차원 그래프다. 방정식을 중학교때 배웠으니 크게 어렵지 않을꺼다. 그래프를 보면 입력에 따라서 출력이 어떻게 분포되어있는지 확인할 수 있다. 그래프를 해석해보자면 입력 X가 작을수록 Y의 값도 작고, 입력 X가 커지면 출력 Y도 따라 커지는 것을 볼 수 있다. 이정도 해석을 내리는 것은 어렵지 않을 것이다. 벌써 선형 회귀를 한 20% 이해한 것이다.

모델

예측값 Y를 찾아낼 수 있는 규칙

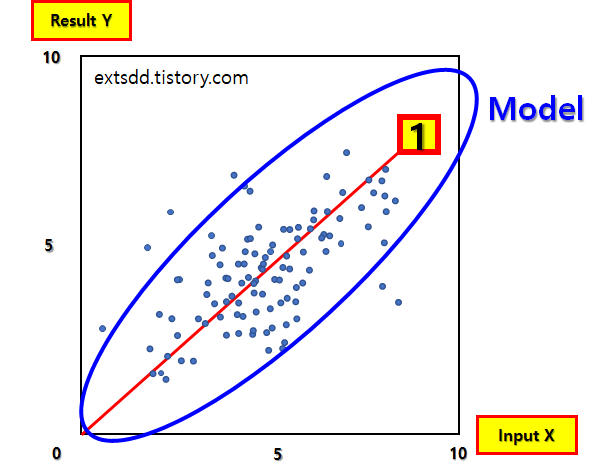
대충 딱 보고 아 우상향으로 점들이 집중해 있으니 사진에 보이는 굵은 실선(1번 선)처럼 점집합들의 대략 중앙을 지나는 선을 그으면 어느정도 예측가능하겠군!! 우리가 딱보고 찾은 규칙은 대략 y=x라는 것이다. 눈으로 찾은것이기 때문에 정확하게 계산하면 오차는 있겠지만 머 대충 입력에 7이 들어오면 출력이 7언저리가 나오겠네 예측이 가능하다. 저 빨간 실선이 바로 모델이고 우린 두눈으로 한눈에 최적의 모델을 찾아버린 것이다.

​

자 우리는 규칙을 찾았다. 인간의 뇌는 참 대단하다. 머릿속으로 복잡한 사고판단도 없이 딱 그래프 1초 보고 규칙을 찾아낼 수 있다. 중요한건 우리가 찾았다는 것이다. 우리가 찾은건 아무 소용이 없다. 머신러닝은 기계 즉 컴퓨터가 저 규칙을 찾게하는 것이다. 그럼 어떻게 찾아야할까? 어떻게는 나중에 생각하고 일단 우리가 뭘 해야하는 지는 알아냈다. 바로 저 점 밀집들의 거의 중앙을 지나가는 최적의 선을 찾는것!

​

선형 (Linear)의 의미

규칙이 선형인 1차원 방정식으로 표현 됨

$y=ax+b$y=ax+b​

위에서 말한 내용을 보면 선형 회귀의 목표는 저 빨간 1번 선을 찾는 거라고 했다. 2차원 그래프에서 저 빨간 선을 표현하는 수식은 y=ax+b 이다. 이건 진짜 중1때 배웠다. a는 기울기고 b는 절편이다. 즉 기울기 a와 절편 b를 찾는게 이 모델의 목표인거고, 선형회귀라는 이름에서 선형은 2차원 그래프로 표현할 수 있는 입력x와 출력y와의 관계에서 1차원 방적식을 표현한 직선이 선형으로 이루어져 있다는 것이다.

​

이제 선형 회귀중 선형의 의미를 알아냈고, 이 선형회귀 모델에서 무엇을 해야하는지 알아냈으니(선형 그래프 기울기a와 절편b를 찾아야함!) 이제 아까 잠시 킵해뒀던 '어떻게'에 대해서 생각해보자. 이 어떻게를 이해하면 이제 회귀라는말이 왜 쓰였는지도 이해가 갈 것이다.

경사하강법 (Gradient Descent)

기울기를 조절하여 모델을 최적화 하는 알고리즘

한가지 아이디어가 있다! 컴퓨터한테 대략 아무 선(랜덤)이나 하나 딱! 그어놓고 가령 예를들어 1번 점선처럼 말이다. 그리고 천천히 기울기a 와 절편 b를 조절하여 3번 실선을 찾는것이다!

​

엥? 뭐야 장난치냐! 이게뭔 머신러닝이야! 할 수도 있는데.. 그만큼 쉬운 머신러닝 모델이다. 사실 따지고보면 아까 우리가 1초만에 눈으로 규칙을 찾았듯이 눈으로 보니까 쉽지. 실제로 코드를 입혀서, 저 수치들을 조절하고, 최적의 직선을 찾는 과정을 보면 그리 쉽지는 않다.

​

자 눈으로도 보이듯이 경사가 점점 내려가면서 점점점~ 점들의 집합을 관통하는 직선으로 이동하게 된다. 이게 바로 경사 하강법! 짝짝짝

회귀 (Regression) 의 의미

자 우리가 아는 회귀의 의미가 뭘까? 다시 돌아오다. 머 이정도로 알고있을 것이다. 혹시 평균으로 부터의 회귀라는 말도 들어보았는가? 평균으로 돌아가려는 성질인데 쉽게 말하면 이런거다. 주사위를 3번 던졌다 6이 2번 나왔고 세번째 던질 차례인데, 6이 많이 나왔다고 3번째에 6이 나올 확률이 줄어들까? 아니다. 매 순간마다 확률은 평균으로 돌아간다.

이해가 안간다면 두번째 예시도 있다. 키작은 부모들의 자식들은 평균적으로 키가 작고 키큰 부모의 자식들은 평균적으로 키가 크다. 만약 평균으로 회귀가 일어나지 않는다면 키큰 부모들 밑에서 태어난 자식들은 한없이 키가 커지고, 반대로 키작은 부모 밑에서 태어난 자식들은 한없이 키가 작아진다. 이렇게 되면 결국 세대를 거듭할수록 인간들은 엄청 큰사람들과 엄청 작은사람들로 나뉘어 질텐데 실제로는 그렇지가 않다.

​

왜냐면 자연에서는 이런 특성이 평균으로 돌아가고 있기 때문이다. 집단이 클수록, 세대를 거듭할수록 이런 특성들은 평균으로 돌아간다. 그래서 우리의 키는 비슷한 것이다.

​

이제 회귀의 의미를 알았을까? 즉 자연의 모든 특성들은 평균으로 회귀하는 특성을 가지고 있기 때문에, 우리가 모점들을 최적으로 지나는 직선을 찾아내면 이 평균으로 회귀하려는 특성을 이용해, 입력 X를 넣으면 Y를 예측 할 수있는 것이다. 왜냐면 모든 특성은 평균으로 회귀하는 특성을 가지고 있으니까!!

​

대충 선형그래프만 하나 구해서 입력으로 떤지면 인간들의 평균키가 유지되듯이 대충은 그 직선과 비슷하게 결과가 나온다는 것!

​

여기까지 우리는 선형 + 회귀에 대한 의미를 이해했다. 이제 실습을 통해서 어떻게 이런 모델을 코드로 만들 수 있는지 직접 만들어보자! 원래 한포스팅에 다 쓸려고 했는데.. 벌써 새벽2시라서 내일 써야겠다..

​

​